

------------------------------------------------------------------------
BIOWULF'S MATHEMATICAL TOOLS:
-----------------------------
NEW BREAKTHROUGHS IN MACHINE LEARNING
-------------------------------------
screenplay by
Alan B. Scrivener
19 July 2001
second draft
------------------------------------------------------------------------
S-___. TITLE CARD
BIOWULF LOGO


| rat # | Carb. | Fat | Cholest. | Sodium | Protein | Vitamin A | Vitamin C | Calcium | Iron | +/- |
|---|---|---|---|---|---|---|---|---|---|---|
| rat #1 | 0 g | 0.5 g | 30 mg | 200 mg | 13 g | 0% | 0% | 0% | 2% | - |
| rat #2 | 20 g | 0 g | 0 mg | 10 mg | 1 g | 0% | 20% | 0% | 2% | - |
| rat #3 | 25 g | 2 g | 0 mg | 45 mg | 0 g | 0% | 0% | 0% | 2% | - |
| rat #4 | 4 g | 0 g | 0 mg | 0 mg | 1 g | 4% | 8% | 2% | 4% | + |
NARRATOR (CONTINUING)
.. and for each rat, they made a list of all of the nutrients
it received, and a notation as to whether it lived or died.
You can see on the list here, each row is a rat. The leftmost
column gives the rat number, the columns in the middle are the
nutrients, and the last column is a plus if the rat lived and
a minus if it died.
S-___. MEDIUM SHOT: NARRATOR IN FRONT OF NEUTRAL BACKGROUND
NARRATOR
The challenge then is to figure out from the list -- and only
from the list -- what is the best diet to feed the rats.
And to be able to take a proposed diet and predict whether
a rat will live or die on it.
S-___. MEDIUM SHOT: NARRATOR IN FRONT OF NEUTRAL BACKGROUND
NARRATOR (CONTINUING)
We want to produce the formula automatically from the numbers
in the list. In other words, we need a program that gets
trained by the data and then can classify new data.
The second example is not made up, but represents actual
research done by BIOwulf's mathematicians.
We were fortunate to receive 62 frozen tissue samples from
____ hospital that were biopsies of patients with suspected
colon cancer. Along with the samples was a file on each
patient covering 30 years of follow-up testing, so that it
was possible for each sample to know the "right answer" in
advance -- whether the patient got colon cancer or not.
With modern genetic analysis techniques we were able to
subject each sample to 2000 gene probes, to determine for
each of 2000 genes whether that gene was silent, active or
hyperactive in the sample. In each case this was turned
into a number from zero to one.
S-___. CARD: TABLE T-3
| patient # | income | gene #1 | gene #2 | gene #3 | gene #4 | *** | +/- |
|---|---|---|---|---|---|---|---|
| patient #1 | 0.56 | 0.45 | 0.55 | 0.21 | 0.98 | *** | - |
| patient #2 | 0.66 | 0.89 | 0.47 | 0.82 | 0.38 | *** | + |
| patient #3 | 0.01 | 0.09 | 0.66 | 0.63 | 0.54 | *** | + |
NARRATOR (CONTINUING)
You can see that for each patient we have a row of data on
which genes were expressed, and by how much, and in the rightmost
column a plus sign if the patient got colon cancer and a minus
if they didn't.
S-___. MEDIUM SHOT: NARRATOR IN FRONT OF NEUTRAL BACKGROUND
NARRATOR (CONTINUING)
Once again the goal is to produce a formula -- what we
call the Decision Function -- to sort patients correctly
into those who will and won't get the cancer, using only
the information on the list.
Okay, a third example: this one is also made up, but it's
designed to help you visualize what's going on more
easily.
This one is really simple. There's only two columns in the chart.
In fact, I'm not even going to show you a chart for this one.
You're sick of charts anyway, right?
Imagine there's this landscape someplace that youy can't see.
Some mountains, valleys, water, and you're trying to avoid the
water, but you have no idea what the shape of the terrain is.
So you drop probes. Each probe tells you its latitude and
longitude. If we assume the earth is flat that's just 2
dimensional grid coordinates. And we also find out if the
probe got wet or not. We get -- guess what? -- a plus if
it's dry and a minus if it's wet.
S-___. CARD: FIGURE F-__



| rat # | Carb. | Fat | Cholest. | Sodium | Protein | Vitamin A | Vitamin C | Calcium | Iron | +/- |
|---|---|---|---|---|---|---|---|---|---|---|
| rat #1 | 0 g | 0.5 g | 30 mg | 200 mg | 13 g | 0% | 0% | 0% | 2% | - |
| rat #2 | 20 g | 0 g | 0 mg | 10 mg | 1 g | 0% | 20% | 0% | 2% | - |
| rat #3 | 25 g | 2 g | 0 mg | 45 mg | 0 g | 0% | 0% | 0% | 2% | - |
| rat #4 | 4 g | 0 g | 0 mg | 0 mg | 1 g | 4% | 8% | 2% | 4% | + |
NARRATOR (CONTINUING)
From this admittedly small sample rat #4 is the only survivor.
It might help to know that rat #4 was fed canned string beans.
It is also tempting to make guesses based on human nutritional
needs, or -- even better -- the needs of other known rats.
S-___. MEDIUM SHOT: NARRATOR IN FRONT OF NEUTRAL BACKGROUND
NARRATOR (CONTINUING)
But there is a big problem with this. You will recall that
there are 2000 genes represented in the tissue samples.
For some of the experiments we haven't talked about yet
there can be up to 22,000 columns of data.
It was Lenin who said, "Quantity has a quality all its own."
Human intuition and judgment are very good at operating on
dozens or maybe even sometimes hundreds of factors, but
thousands of them overwhelm us.
So we put all the information we think might be relevant in
the table. Age, weight, number of known relatives with
similar cancers, all could be added to the patient data.
But then we have to let a computer program do the learning
and the deciding, because the problem is simply too big for
the human mind. One of the things we want the computer to do
is tell us which columns we can toss out -- which ones aren't
needed to create the decision function.
S-___. FIGURE F-1
| _ |
So here in a nutshell is how machine learning is done.
You have some data like the examples above where you know
the right answer. Typically, you break these into two groups,
a training group and a testing group. You run all the
training data through a machine learning program and it
"learns" by coming up with a formula for classifying the
data, which we call a decision function. Built into that
function is the information about which columns n the table
which to throw out.
Next you run the testing data through the decision function
and see if it gets the right answer. When it all seems to
be working correctly you can real data through -- in other
words, data without the pluses and minuses, without the
right answers supplied. That's when you have to wait 30
days and see if the rat dies, or 10 years to see if the
credit card customer pays their bills, or 30 years to see
if the patient gets colon cancer.
S-___. MEDIUM SHOT: NARRATOR IN FRONT OF NEUTRAL BACKGROUND
NARRATOR (CONTINUING)
The only other complication is that usually you really don't just
want pluses and minuses, it would be nice to know how sure
you are, so the decision function usually returns a number. If
the number is positive, that's a plus, and if it's negative,
that's a minus, and the magnitude tells us the confidence.
So there you have machine learning in a nutshell -- at least
the problem definition. The hard work comes in trying to
design a program which can turn the training examples into the
decision function, and that's what the rest of this video is
about.
.
For the last 50 years or so the most popular traditional approach
to the machine learning problem has been to use neural networks...
S-___. FIGURE F-2: PHOTO OF NEURONS

|
NARRATOR (CONTINUING)
... This involves simulating the actual neurons in the human
nervous system, and this approach has done a pretty good job.
But as we will see, the "SVM" method does better in many cases.
To continue the terrain metaphor, neural nets can find hills and
valleys, but they don't always find the highest hill or the
deepest valley.
S-___. MEDIUM SHOT: NARRATOR IN FRONT OF NEUTRAL BACKGROUND
NARRATOR (CONTINUING)
But before I can explain the SVM method, I need to introduce a
few more concepts.
S-___. CARD YELLOW LETTERS ON BLUE BACKGROUND:
generalization
NARRATOR (CONTINUING)
Generalization.
S-___. MEDIUM SHOT: NARRATOR IN FRONT OF NEUTRAL BACKGROUND
NARRATOR (CONTINUING)
If a learning machine doesn't generalize, it is useless.
The whole point is to form generalizations that can be used
to make new decisions. For that reason it is important to
find some kind of generlaized portrait of the data boundary,
the water line if you will.
S-___. CARD YELLOW LETTERS ON BLUE BACKGROUND:
overfitting
NARRATOR (CONTINUING)
Overfitting.
S-___. MEDIUM SHOT: NARRATOR IN FRONT OF NEUTRAL BACKGROUND
NARRATOR (CONTINUING)
This is the thing we want to avoid. It's sort of like overreacting
to clues, or getting too hung up on details. When a learning
machine gets too specific, and thinks only certain exacxt data
values are in plus territory, overfitting has occured.
S-___. CARD YELLOW LETTERS ON BLUE BACKGROUND:
state space
NARRATOR (CONTINUING)
State space.
S-___. MEDIUM SHOT: NARRATOR IN FRONT OF NEUTRAL BACKGROUND
NARRATOR (CONTINUING)
Normally when we use the word space we're talking about the
space that fills the universe we live in. We usually call
it a three-dimensional space, because we can specify a point
in it with three coordinates. This GPS...
S-___. CLOSE-UP: NARRATOR HOLDING UP GPS
NARRATOR (CONTINUING)
... a Global Positioning System receiver, tells me my latitude
north or south, my longitude east or west, and my elevation.
This completely defines my position in 3D space.
Sometimes people say time is the fourth dimension, so the GPS
also tells time, which locates my in the 4th dimension as well.
S-___. MEDIUM SHOT: NARRATOR IN FRONT OF NEUTRAL BACKGROUND
NARRATOR (CONTINUING)
But mathematicians like to think about lots of other
spaces besides physical space. A state space is an imaginary
space where each point represents a possible state of a system.
They have lots of uses, but the way we're going to use them
here is to represent rows in out data lists. To start with,
let's pretend all of our data has only two columns of values
for each row. That will allow us to represent each row -- each rat
or patient or probe -- as a point in a two-dimensional state space.
S-___. CARD: FIGURE F-3
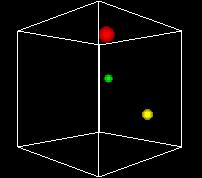
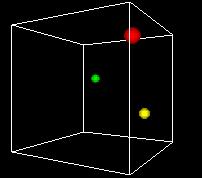
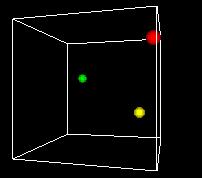
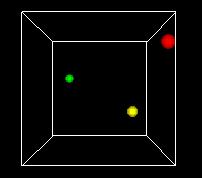
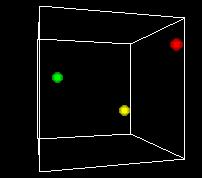
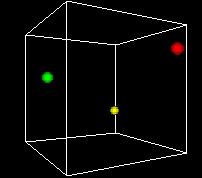
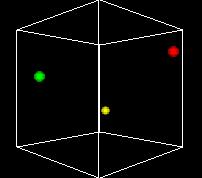
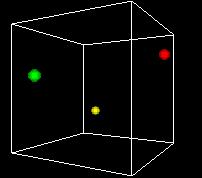
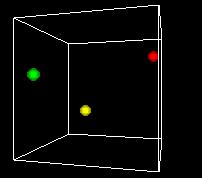
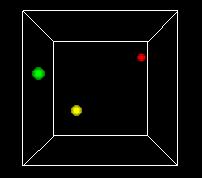 NARRATOR (CONTINUING)
This animation shows the space turning so we can get views
from different angles. One of the problems of the 3D view
is can be hard to see what's behind. Using time as an added
dimension and turning a model can help solve this problem
if we only want to see a few points in the state space.
But if we want to plot every possible point, we can't see
a whole volume of points directly, any more that we can
see inside a stack of pingpong balls..
A more fundamental problem is that -- remember -- we have up
to 22,000 dimensions in our data. We're already hitting some
problems with 3 dimensions, and we've run out. Clearly we can't
directly visualize higher-dimensional state spaces. But there
are some tricks we can do, as we'll see later.
Still another problem is that we want to be able to display
our decision function, the output of the Support Vector Machine
method. It's just a one-dimensional function, but that does
use a dimension.
So the most common approach is like the one in this figure...
S-___. CARD: FIGURE F-4
NARRATOR (CONTINUING)
This animation shows the space turning so we can get views
from different angles. One of the problems of the 3D view
is can be hard to see what's behind. Using time as an added
dimension and turning a model can help solve this problem
if we only want to see a few points in the state space.
But if we want to plot every possible point, we can't see
a whole volume of points directly, any more that we can
see inside a stack of pingpong balls..
A more fundamental problem is that -- remember -- we have up
to 22,000 dimensions in our data. We're already hitting some
problems with 3 dimensions, and we've run out. Clearly we can't
directly visualize higher-dimensional state spaces. But there
are some tricks we can do, as we'll see later.
Still another problem is that we want to be able to display
our decision function, the output of the Support Vector Machine
method. It's just a one-dimensional function, but that does
use a dimension.
So the most common approach is like the one in this figure...
S-___. CARD: FIGURE F-4

 from http://www.agso.gov.au/geophysics/date050397.html |
NARRATOR (CONTINUING)
That's how the government of Australia produced this image.
Ranges of altitudes are shown, starting at sea level, as blue,
light blue, green, yellow, orange, red, violet and gray for
the highest.
This is just another way to show terrain data -- or state space data.
[PAUSE]
S-___. MEDIUM SHOT: NARRATOR IN FRONT OF NEUTRAL BACKGROUND
NARRATOR (CONTINUING)
So let's see some decision function data plotted this way.
S-___. FIGURE F-6
 |
NARRATOR (CONTINUING)
Here is a decision function for some 2D data, where
dark blue is for the lowest negative values and dark
red is for the highest positive values. The black
line is where the decision function is zero, and so the
data is "right on the line" between +, live rat or good
credit, and -, dead rat or bad credit.
S-___. MEDIUM SHOT: NARRATOR IN FRONT OF NEUTRAL BACKGROUND
NARRATOR (CONTINUING)
Remember, we're trying to show some analogies here by
boiling 22,000 dimensions of data down to 2, and then
using the third for the decision function. And I want to
emphasize that we do this not because it's a great ideas,
but because we don't know of a better way to display
these fundamental concepts. If we knew how to display
the 22,00 dimensions without boiling anything down we'd
certainly prefer it.
One thing this exercise does illustrate is the
importance of reducing dimensions if you can.
Many techniques in machine learning, including SVMs,
begin by attempting to eliminate as many dimensions
-- in other words as many columns of data -- as possible
without sacrificing quality in the decision function.
In fact, recent research by BIOwulf mathematicians
has shown that coming up with which columns to throw out
is actually more critical than coming up with an otherwise
good decision function. So we'll look at tossing out
columns first.
Assume we have some sort of workable program for creating
decision functions from training data. The most
straightforward approach would be to try every possible
subset of columns and each time, produce the decision
function using the training data and then test it using
the testing data. The find the smallest subset that
gives right answers. Simple!
Unfortunately, it's also impossible in a practical sense,
because of something called the combinatorial explosion.
S-___. CARD YELLOW LETTERS ON BLUE BACKGROUND:
combinatorial explosion
NARRATOR (CONTINUING)
To understand the combinatorial explosion, let's take a
momentary diversion into the world of subsets.
S-___. MEDIUM SHOT: NARRATOR IN FRONT OF NEUTRAL BACKGROUND
NARRATOR (CONTINUING)
First lets consider some small sets and their subsets. If you
have a set with only one thing in it, there are two possible
subsets: the original set with one thing in it and the
empty set, which you will recall is the name for a set with
nothing in it.
S-___. ANIMATION A-2
NARRATOR (CONTINUING)
This animation is cycling through these two options.
One thing, then nothing. Or if you prefer, nothing,
then one thing. The sphere is the one object, and
we use red to show not being in the set and green to
show being in the set. Just like red means stop and
green means go at a traffic light, here red means "no"
and green means "yes."
So far with this example it is no problem to just breeze
through all the combinations.
S-___. ANIMATION A-3
NARRATOR (CONTINUING)
Next consider a set of two objects. There are four subsets:
no objects, one object, the other object, or both objects.
We highlight the connection between them to emphasize that
they are in a subset together.
S-___. MEDIUM SHOT: NARRATOR IN FRONT OF NEUTRAL BACKGROUND
NARRATOR (CONTINUING)
So one object had 2 subsets, while 2 objects had 4 subsets.
What do you think, will 3 objects have 6 subsets?
S-___. ANIMATION A-4
NARRATOR (CONTINUING)
As you can see in this animation, there is one way to take
no things, three ways to take one thing, three ways to
take two things, and one way to take three things.
That adds up to eight subsets.
S-___. MEDIUM SHOT: NARRATOR IN FRONT OF NEUTRAL BACKGROUND
NARRATOR (CONTINUING)
Eight? The sequence goes 2, 4, 8 so far. Is it doubling
every time? Let's see.
S-___. ANIMATION A-5
NARRATOR (CONTINUING)
Sure enough. When there are four objects, there is
one way to have no thing, four ways to have one thing,
six ways to have two things -- four around the square
and the two diagonals -- four ways to have three things
and one way to have four things.
S-___. MEDIUM SHOT: NARRATOR IN FRONT OF NEUTRAL BACKGROUND
NARRATOR (CONTINUING)
This is getting boring. You know why? Because it's
taking so long! It is doubling every time. That was
sixteen subsets, and the next one, seven objects, would
be 32 subsets. So we're not going to do that one. At the
2 frames per second we've been using, it would take over
a minute. We promised this would be short.
So let's jump ahead. What if we have 30 objects?
That's not a very big number. A classroom of 30
students is a common thing. How many possible
clubs could you form out of a classroom of thirty
students? If we try to count them up I don't think
we'll make it.
S-___. ANIMATION A-6
| * * * |
NARRATOR (CONTINUING)
It starts out easy -- there's one way to have a club
with no students. Thirty ways to have a club with one student.
335 ways to have a club with 2 students. This is going
to take a while. Almost 3 minutes just for the clubs of two
students. While we're watching the animation run, let me talk
about how we figure this out. There's 30 ways to pick the
first student, and because they can't be in a club twice you
exclude them from the second choice, and have 29 ways to pick
the second student. But that means we've counted each club twice,
so the formula is 30 times 29 divided by 2, which is how we get 335.
As you can imagine, this is quite a pain to do for all the sizes of
clubs.
Luckily there's another way. If it doubles each time, the
general rule is that the number of subsets is just 2 to the
power of the number of objects. Call this N for number of
objects. The number of subsets is 2 raised to the N power.
2 raised to the 30th power is over a billion (that's American
billion, 1 followed by 9 zeroes). At this frame rate it will take us
17 years to watch this animation. So get comfy!
Just kidding.
[ANIMATION IS INTERRUPTED]
S-___. MEDIUM SHOT: NARRATOR IN FRONT OF NEUTRAL BACKGROUND
NARRATOR (CONTINUING)
Now you can see why we call it a combinatorial explosion.
Remember, we're dealing with data with up to 22,000 things to
correlate in subsets. Long before we get up that high
we'll be dealing with more susbsets than there are particles
in the known universe. People like to use that phrase a lot:
"more than the number of particles in the known universe."
But that's just peanuts to the combinatorial explosion. These
numbers are staggeringly bigger than that!
Allow me to quote from Douglas Adams, in The Hitchhiker's
Guide to the Galaxy.:
[HOLDS UP BOOK]
"Space is big. Really big. You just won't believe how
vastly hugely mind-bogglingly big it is. I mean, you may
think it's a long way down the road to the chemist, but
that's just peanuts to space."
Well, as you know, space is mostly devoid of matter -- the
known universe is mostly empty space. But imagine if the same
sized known universe was full of particles, as many as it could
hold. The number of subsets of 22,000 objects is mind-numbingly
bigger than the number of particles the universe could hold.
So my point, and I do have one, is that because of the
combinatorial explosion there is no way we are going
to try all possible subsets of what we are calling the
columns or the dimensions of data. So, we have to do
something else. Something smarter.
Now that we've returned from our diversion through the world
of subsets, our next concept is...
S-___. CARD YELLOW LETTERS ON BLUE BACKGROUND:
correlation
NARRATOR (CONTINUING)
...correlation. One of the most important questions
people can ask is, "why?" We want to establish causality.
The first step in that process is to establish a correlation.
S-___. CARD: FIGURE F-7


|
Table 1.1
|
| . | . | . | Linear | . | . | . | . | Nonlinear | . |
|---|---|---|---|---|---|---|---|---|---|
| Equation Type: | One Equation |
. | Several Equations |
. | Many Equations |
. | One Equation |
Several Equations |
Many Equations |
| Algebraic | Trivial | . | Easy | . | Essentially Impossible | . | Very Difficult | Very Difficult | Impossible |
| Ordinary Differential | Easy | . | Difficult | . | Essentially Impossible | . | Essentially Impossible | Impossible | Impossible |
| . | . | . | x | . | . | . | . | . | . |
| Partial Differential | Difficult | . | Essentially Impossible | . | Essentially Impossible | . | Impossible | Impossible | Impossible |
* Courtesy of Electronic Associates, Inc.
NARRATOR (CONTINUING)
Take a moment to look at this. Down the left column are
listed types of equations. Of the other two columns to
the right, one is for linear and the other for non-linear
equations. [PAUSE]
Notice that all the non-linear equations are very
difficult or worse. Even the linear equations are pretty
bad. Everything to the right of the thick black line is
pretty useless.
S-___. MEDIUM SHOT: NARRATOR IN FRONT OF NEUTRAL BACKGROUND
Here's what the author had to say in his own dryly
humorous style: "[these equations are], if linear,
tiresome to solve even in the case of a few variables;
if nonlinear, they are unsolvable except in special cases."
So, to paraphrase an old song, we will use linear
equations when we can and non-linear equations when we must.
S-___. CARD YELLOW LETTERS ON BLUE BACKGROUND:
weights
NARRATOR (CONTINUING)
Building on the concept of linearity, our next
concepts is weights.
S-___. MEDIUM SHOT: NARRATOR IN FRONT OF NEUTRAL BACKGROUND
NARRATOR (CONTINUING)
Our best hope is that we can produce a linear decision
function, with weights for each data dimension. We
use the term weights to mean a set of constants, like
'a' in the last example, only a vector of them. We call
this vector 'w' for weights, and it consists of a set of
constants named w-sub-1 through w-sub-22,000 or whatever.
So our decision function d becomes this.
S-___. CARD YELLOW LETTERS ON BLUE BACKGROUND:
vector form
D = w.x
expanded
D = w1 x1 + w2 x2 + w3 x3 +
NARRATOR (CONTINUING)
We use bold in the vector form to show that w and x are vectors.
The w's and x's in the expanded form are the components of the
vectors.
S-___. MEDIUM SHOT: NARRATOR IN FRONT OF NEUTRAL BACKGROUND
NARRATOR (CONTINUING)
We can visualize each x vector as a bunch of strips of cloth
tied onto a string to become the tail of a kite.
S-___. MEDIUM SHOT: NARRATOR WITH KITE
NARRATOR (CONTINUING)
Didi you get that? One vector is a kite tail, with lots of cloth strips. Each cloth strip stands for a number. They're called components of the vector. One kite, one vector. And remember, there will be lots of vectors.
Each kite tail lands, in turn, next to the same set of weight
values as you see in this animation...
S-___. ANIMATION A-8
[Note: Again, in this animation the narrator's finger should be
represented on a dial or knob, or else editing should be
used to incorporate live action of the narrator moving
a mouse.]



| rat # | Carb. | Fat | Cholest. | Sodium | Protein | Vitamin A | Vitamin C | Calcium | Iron | +/- |
|---|---|---|---|---|---|---|---|---|---|---|
| rat #1 | 0 g | 0.5 g | 30 mg | 200 mg | 13 g | 0% | 0% | 0% | 2% | - |
| rat #2 | 20 g | 0 g | 0 mg | 10 mg | 1 g | 0% | 20% | 0% | 2% | - |
| rat #3 | 25 g | 2 g | 0 mg | 45 mg | 0 g | 0% | 0% | 0% | 2% | - |
| rat #4 | 4 g | 0 g | 0 mg | 0 mg | 1 g | 4% | 8% | 2% | 4% | + |
NARRATOR (CONTINUING)
Recall our table of which nutrients the rats were fed. We
called the rows in this table data points, points in the
state space, vectors, and sometimes test data or training
data. We called the columns in this tables variables,
dimensions and features. They're dimensions when we want
to represent them in a state space, and features when we
want to eliminate them with recursive feature elimination.
Now we're going to call them dimensions again as we do some
math tricks with them.
S-___. ANIMATION A-9
[NOTE: THIS FOOTAGE HAS ALREADY BEEN PRODUCED BY BEOWULF]




















Written, Directed and Edited by Alan Scrivener.
Narrated by Mollie Tobin.
Computer graphics by Alan Scrivener.
Geographical visualizations by Jeff Sale.
Special thanks to Wayne Holder and Bob Zawalnicki.
Produced by Human Interface Prototypes
for Mindtel Corp.
Filmed at the San Diego Public Library,
Mission San Diego de Alcala,
and Mission Trails Regional Park,
San Diego, California.
(C) 2001 Mindtel Corp.
Keep wondering.
Last update 19-Jul-2001 11:59 PM PDT by ABS.